[5]:
import straph as sg
import matplotlib.pyplot as plt
[6]:
plt.rcParams["figure.figsize"] = (12,9)
Connected Components¶
Connected components are among the most basic, useful and important concepts of graph theory. It is common usage to decompose a graph into its connected components. If a graph is not connected, it can be divided into distinct connected components. Many properties, which involve computation of paths or communities, can be computed independently on each connected component, thus enabling parallel execution of numerous methods.
Connected components were recently generalized to stream graphs. These generalized connected components have a crucial feature: like graph connected components and unlike other generalizations available in the literature, they partition the set of temporal nodes. This means that each node at each time instant is in one and only one connected component. This makes these generalized connected components particularly appealing to capture important features of the vast variety of objects modeled by stream graphs.
[7]:
path_directory = "examples/"
S = sg.read_stream_graph(path_nodes=path_directory + "example_nodes.sg",
path_links=path_directory + "example_links.sg")
Weakly Connected Components¶
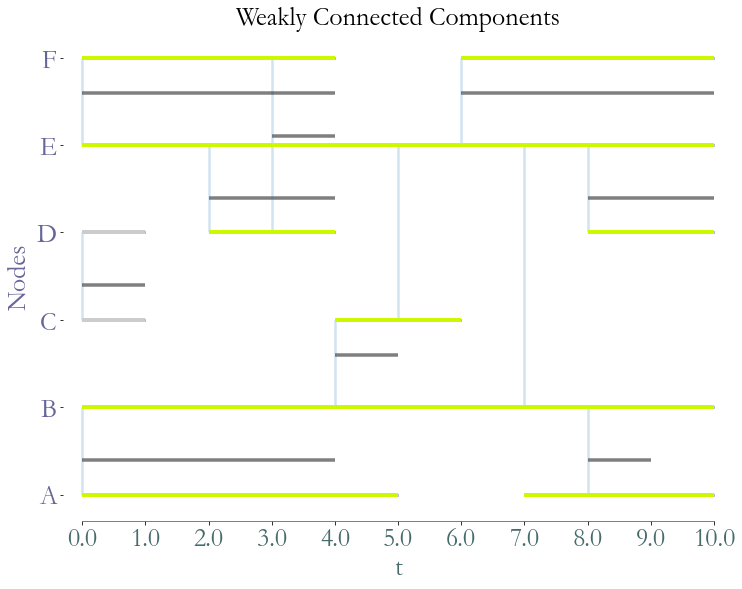
In a Stream Graph, 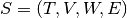 , weakly connected components represent elements
of
, weakly connected components represent elements
of 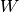 connected together without any constraint on time.
connected together without any constraint on time.
Intuitively, the weakly connected components correspond to the disconnected parts of a drawing of a stream graph.
[8]:
wcc = S.weakly_connected_components()
_ = S.plot(clusters=wcc,title="Weakly Connected Components")
These elements can be analysed separately to observe and compute some properties, allowing a parallel implementation of several methods.
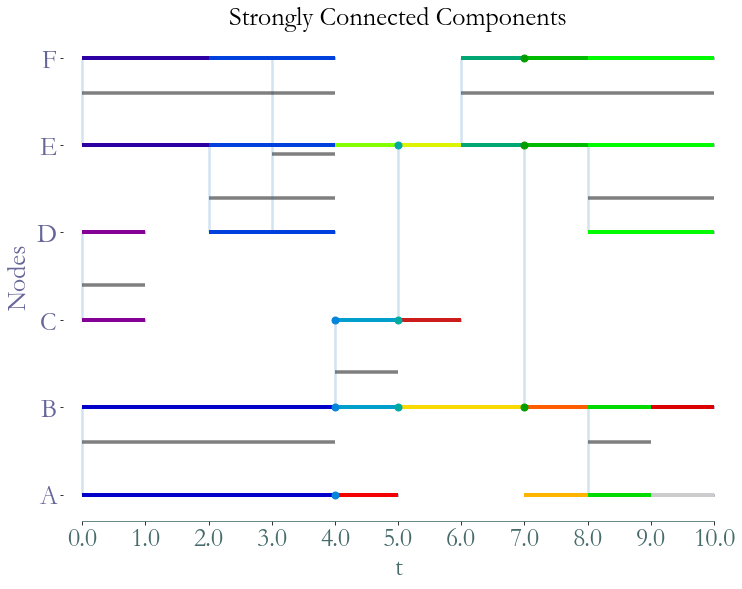
Strongly Connected Components¶
Inside a strongly connected component all nodes are reachable from any other at any time instant.
This definition is consistent with the one used in graph theory: for any time instant, if we
take the induced Graph  the SCC at
the SCC at 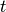 corresponds to the
connected components of
corresponds to the
connected components of 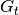 .
.
[9]:
scc = S.strongly_connected_components(format = "cluster")
_ = S.plot(clusters=scc,title="Strongly Connected Components")
Stable Connected Components¶
A stable connected component is a cluster 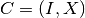 ,
, ![I = [b,e]](../_images/math/b1a96dfb0f672a8f62489cd38224ca64a5a33159.png) ,
,
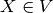 where interactions between the nodes have begun before
where interactions between the nodes have begun before 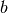 or at the same time and have ended after
or at the same time and have ended after  or at the same
time.
or at the same
time.
The decomposition into stable connected components is a finer grain decomposition of the stream graph than the one into strongly connected components.
A stable connected component, 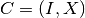 , can be reduced to a static graph
, can be reduced to a static graph 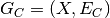 spanning
spanning 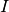 .
.
[10]:
stcc = S.stable_connected_components(format = "cluster")
_ = S.plot(clusters=stcc,title="Stable Connected Components")
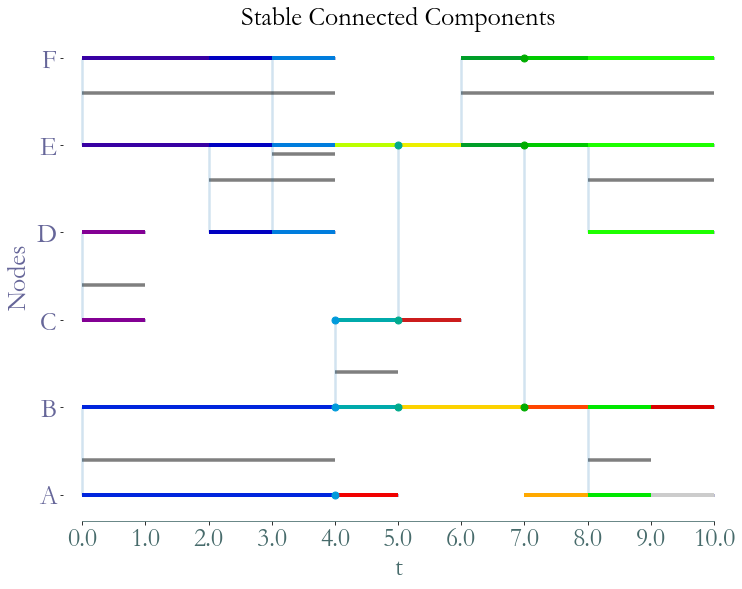
For more details we refer to the paper Connected Components in Stream Graphs.