[1]:
import matplotlib.pyplot as plt
import straph as sg
[2]:
plt.rcParams["figure.figsize"] = (12,9)
Introduction¶
Formally, a stream graph 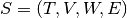 is defined by a set of time instants
is defined by a set of time instants 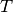 , a
finite set of nodes
, a
finite set of nodes 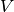 , a set of temporal nodes
, a set of temporal nodes 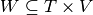 ,
and a set of temporal links
,
and a set of temporal links 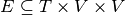 . The set of time
instants
. The set of time
instants 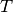 can be continuous or discrete. Likewise interactions (temporal links)
between two nodes can be discrete
can be continuous or discrete. Likewise interactions (temporal links)
between two nodes can be discrete 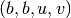 or continuous
or continuous 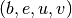 (with
(with 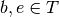 and
and 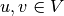 ).
).
Stream graphs can be used to model any connected structure evolving through time. For instance, IP traffic between entities can be modelised as follow: whenever two IP adresses exchanges packets we record a temporal link between these two nodes corresponding to the duration of the exchange.
First of all, we load an artificial example that will be used in the following steps of analysis and visualisation.
[3]:
path_directory = "examples/"
S = sg.read_stream_graph(path_nodes=path_directory + "example_nodes.sg",
path_links=path_directory + "example_links.sg")
Basic visualisation¶
[4]:
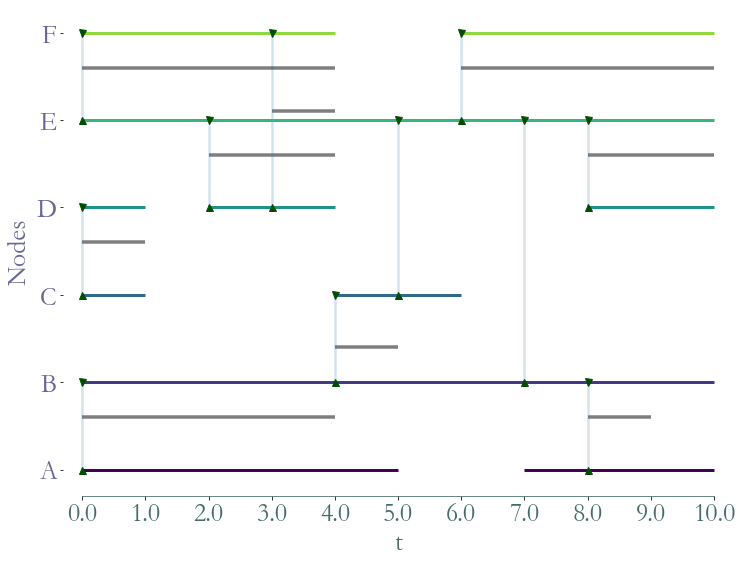
fig = S.plot()
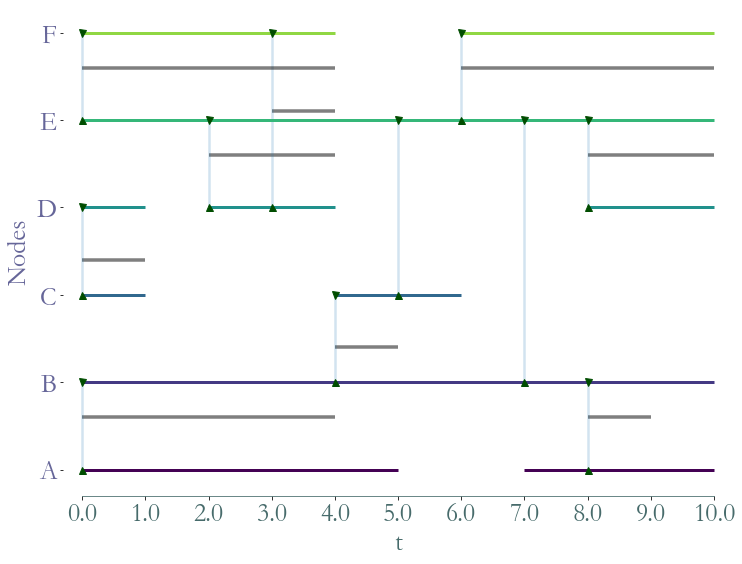
We refer to this Notebook for more details on visualisation.
Stream Graph Object¶
Paradigme: In Straph
simple data structures should be represented by built-in python objects, resulting in a more
comprehensive and intuitive code.
After a comparative analysis we choose to use the following data structures for manipulating
stream graphs. (As numerous algorithms and basic computations are not based on vectorials
operations Numpy
arrays were deemed to slow.)
A StreamGraph
object is constituted by five main attributes:
times: the time window of the stream graph (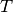 )
)nodes: the list of nodes present in the stream graph (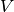 )
)node_presence: a list of list, each list corresponds to a node and contains its presence time (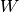 )
)links: the list of links present in the stream graph (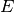 )
)node_presence: a list of list, each list corresponds to a link and contains its presence time (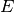 )
)
[5]:
S.times
[5]:
[0.0, 10.0]
The stream graph spans from instant  to
to 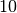
[6]:
S.nodes
[6]:
[0, 1, 2, 3, 4, 5]
S contains 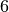 nodes. Nodes are always represented by integers, their labels can be stored in
the attribute
nodes. Nodes are always represented by integers, their labels can be stored in
the attribute node_to_label.
[7]:
S.node_to_label
[7]:
{0: 'A', 1: 'B', 2: 'C', 3: 'D', 4: 'E', 5: 'F'}
[8]:
S.node_presence
[8]:
[[0.0, 5.0, 7.0, 10.0],
[0.0, 10.0],
[0.0, 1.0, 4.0, 6.0],
[0.0, 1.0, 2.0, 4.0, 8.0, 10.0],
[0.0, 10.0],
[0.0, 4.0, 6.0, 10.0]]
As we can see on the above figure, node 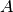 with index
with index  is present
from time
is present
from time  to
to 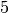 , absent from
, absent from 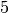 to
to 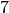 and present again from
and present again from 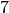 to
to 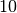 .
.
[9]:
S.links
[9]:
[(0, 1), (1, 2), (1, 4), (2, 3), (2, 4), (3, 4), (3, 5), (4, 5)]
[10]:
S.link_presence
[10]:
[[0.0, 4.0, 8.0, 9.0],
[4.0, 5.0],
[7.0, 7.0],
[0.0, 1.0],
[5.0, 5.0],
[2.0, 4.0, 8.0, 10.0],
[3.0, 4.0],
[0.0, 4.0, 6.0, 10.0]]
The link 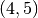 (corresponding to nodes
(corresponding to nodes 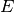 and
and 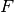 ) with
index
) with
index 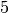 is active from time
is active from time  to
to 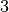 and again from
and again from
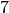 to
to 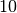 .
.
A short description of a stream graph scale can be obtained with .describe()
[11]:
S.describe()
Nb of Nodes : 6
Nb of segmented nodes : 11.0
Nb of links : 8
Nb of segmented links : 11.0
Nb of event times : 11
We can add or remove nodes and links to/from a stream_graph object
(we refer to this notebook for further information).
We can easily add a new node. Let’s add 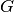 present from
present from  to
to 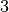 and from
and from 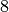 to
to 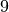 .
.
[12]:
S.add_node('G',[0,3,8,9])
[12]:
6
Likewise we can add a new link. If one of the extrimities is new, it will be added
automatically for the duration of the link. Let’s add a link 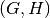 from
from 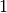 to
to 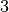 and from
and from 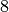 to
to 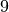 .
.
[13]:
S.add_link(('G','H'),[1,3,8,9])
_ = S.plot()
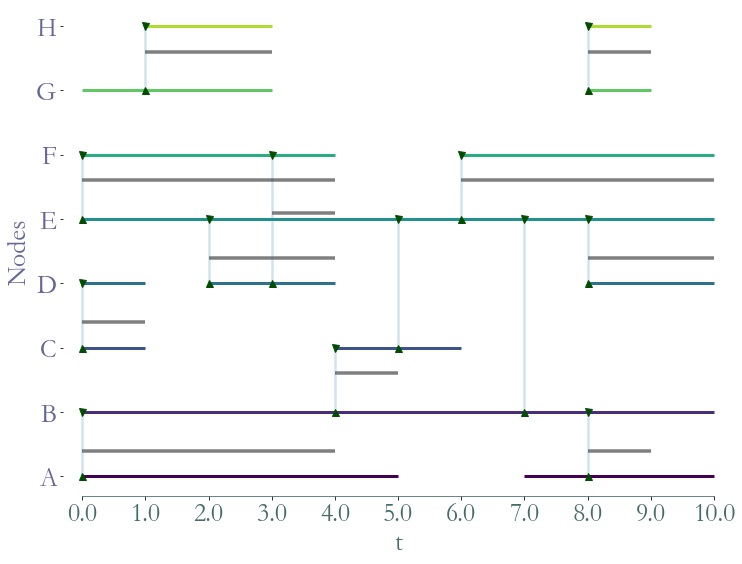
Let’s remove these new interactions between nodes  and
and  .
.
[14]:
S.remove_link(('G','H'))
_ = S.plot()
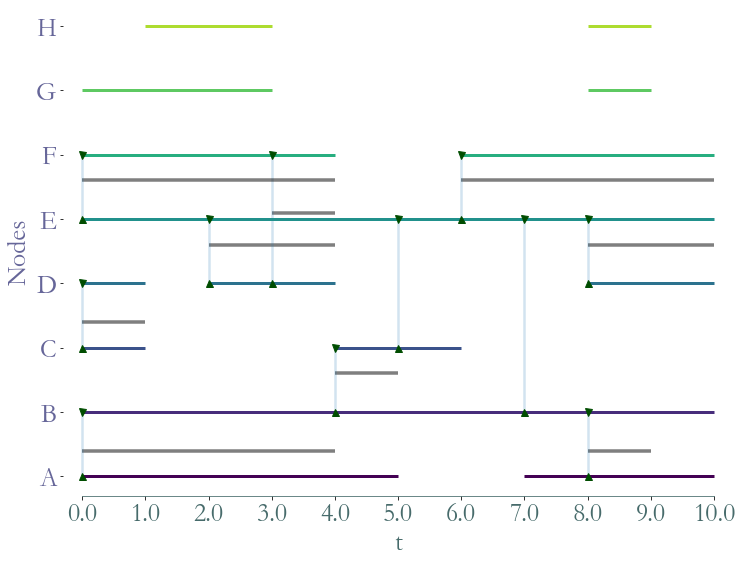
Note : If we remove a node, all of its links will be automatically removed.
[15]:
S.remove_node('G')
S.remove_node('H')
[16]:
S.plot()
plt.show()
Manipulating a Stream Graph Object¶
There are several manners to manipulate a StreamGraph object: - Iterate on nodes - Iterate on links -
Iterate on temporally ordered links - Iterate on temporally ordered events
[17]:
for n,np in zip(S.nodes,S.node_presence):
for b,e in zip(np[::2],np[1::2]): # Even index are arrivals and odd index departure
print("Node ",S.node_to_label[n]," is present from ",b," to ",e)
Node A is present from 0.0 to 5.0
Node A is present from 7.0 to 10.0
Node B is present from 0.0 to 10.0
Node C is present from 0.0 to 1.0
Node C is present from 4.0 to 6.0
Node D is present from 0.0 to 1.0
Node D is present from 2.0 to 4.0
Node D is present from 8.0 to 10.0
Node E is present from 0.0 to 10.0
Node F is present from 0.0 to 4.0
Node F is present from 6.0 to 10.0
[18]:
for l,lp in zip(S.links,S.link_presence):
for b,e in zip(lp[::2],lp[1::2]): # Even index are arrivals and odd index departure
u,v = l
print("Link ",(S.node_to_label[u],S.node_to_label[v])," is present from ",b," to ",e)
Link ('A', 'B') is present from 0.0 to 4.0
Link ('A', 'B') is present from 8.0 to 9.0
Link ('B', 'C') is present from 4.0 to 5.0
Link ('B', 'E') is present from 7.0 to 7.0
Link ('C', 'D') is present from 0.0 to 1.0
Link ('C', 'E') is present from 5.0 to 5.0
Link ('D', 'E') is present from 2.0 to 4.0
Link ('D', 'E') is present from 8.0 to 10.0
Link ('D', 'F') is present from 3.0 to 4.0
Link ('E', 'F') is present from 0.0 to 4.0
Link ('E', 'F') is present from 6.0 to 10.0
[19]:
for e in S.ordered_links():
if e[0] == 1:
_, t0, t1, u, v = e
print("Link arrival \t:",(t0,t1,S.node_to_label[u],S.node_to_label[v]))
if e[0] == -1:
_, t1, u, v = e
print("Link departure \t:",(t1,S.node_to_label[u],S.node_to_label[v]))
Link arrival : (0.0, 4.0, 'A', 'B')
Link arrival : (0.0, 1.0, 'C', 'D')
Link arrival : (0.0, 4.0, 'E', 'F')
Link departure : (1.0, 'C', 'D')
Link arrival : (2.0, 4.0, 'D', 'E')
Link arrival : (3.0, 4.0, 'D', 'F')
Link arrival : (4.0, 5.0, 'B', 'C')
Link departure : (4.0, 'A', 'B')
Link departure : (4.0, 'D', 'E')
Link departure : (4.0, 'D', 'F')
Link departure : (4.0, 'E', 'F')
Link arrival : (5.0, 5.0, 'C', 'E')
Link departure : (5.0, 'B', 'C')
Link departure : (5.0, 'C', 'E')
Link arrival : (6.0, 10.0, 'E', 'F')
Link arrival : (7.0, 7.0, 'B', 'E')
Link departure : (7.0, 'B', 'E')
Link arrival : (8.0, 9.0, 'A', 'B')
Link arrival : (8.0, 10.0, 'D', 'E')
Link departure : (9.0, 'A', 'B')
Link departure : (10.0, 'D', 'E')
Link departure : (10.0, 'E', 'F')
[20]:
for e in S.ordered_events():
if e[0] == 2:
_,t0,t1,u = e
print("Node arrival \t:",(t0,t1,S.node_to_label[u]))
elif e[0] == 1:
_, t0, t1, u, v = e
print("Link arrival \t:",(t0,t1,S.node_to_label[u],S.node_to_label[v]))
elif e[0] == -1:
_, t1, u, v = e
print("Link departure \t:",(t1,S.node_to_label[u],S.node_to_label[v]))
elif e[0] == -2:
_,t1,u = e
print("Node departure \t:",(t1,S.node_to_label[u]))
Node arrival : (0.0, 5.0, 'A')
Node arrival : (0.0, 10.0, 'B')
Node arrival : (0.0, 1.0, 'C')
Node arrival : (0.0, 1.0, 'D')
Node arrival : (0.0, 10.0, 'E')
Node arrival : (0.0, 4.0, 'F')
Link arrival : (0.0, 4.0, 'A', 'B')
Link arrival : (0.0, 1.0, 'C', 'D')
Link arrival : (0.0, 4.0, 'E', 'F')
Link departure : (1.0, 'C', 'D')
Node departure : (1.0, 'C')
Node departure : (1.0, 'D')
Node arrival : (2.0, 4.0, 'D')
Link arrival : (2.0, 4.0, 'D', 'E')
Link arrival : (3.0, 4.0, 'D', 'F')
Node arrival : (4.0, 6.0, 'C')
Link arrival : (4.0, 5.0, 'B', 'C')
Link departure : (4.0, 'A', 'B')
Link departure : (4.0, 'D', 'E')
Link departure : (4.0, 'D', 'F')
Link departure : (4.0, 'E', 'F')
Node departure : (4.0, 'D')
Node departure : (4.0, 'F')
Link arrival : (5.0, 5.0, 'C', 'E')
Link departure : (5.0, 'B', 'C')
Link departure : (5.0, 'C', 'E')
Node departure : (5.0, 'A')
Node arrival : (6.0, 10.0, 'F')
Link arrival : (6.0, 10.0, 'E', 'F')
Node departure : (6.0, 'C')
Node arrival : (7.0, 10.0, 'A')
Link arrival : (7.0, 7.0, 'B', 'E')
Link departure : (7.0, 'B', 'E')
Node arrival : (8.0, 10.0, 'D')
Link arrival : (8.0, 9.0, 'A', 'B')
Link arrival : (8.0, 10.0, 'D', 'E')
Link departure : (9.0, 'A', 'B')
Link departure : (10.0, 'D', 'E')
Link departure : (10.0, 'E', 'F')
Node departure : (10.0, 'A')
Node departure : (10.0, 'B')
Node departure : (10.0, 'D')
Node departure : (10.0, 'E')
Node departure : (10.0, 'F')
In Straph almost
all algorithms are based on these data structures.